
LE MASQUE FLOU EN IMAGERIE NUMERIQUE (2/4)
David ROMEUF - 1993 - romeuf@ocar01.obs-azur.fr
Article paru dans les numéros 711 et 712 de Novembre-Décembre 95 & Janvier-Février 1996 de la revue PULSAR - SAP



III - Principe général du masque flou en imagerie numérique
VII - Une méthode de traitement des détails
VIII - La réduction des artefacts
Le masque des détails est quantifié sur beaucoup moins de niveaux que l'image prétraitée puisqu'il s'agit d'écarts. Enfin, il contient les détails d'au moins l'échelle que l'on a voulu extraire (en pixels). Pour obtenir l'image finale où les détails souhaités seront mieux visibles qu'avant, il suffit alors d'ajouter l'image des détails à l'image initiale prétraitée. On peut rendre le masque de détails plus efficace en le multipliant par une constante. Voici la formule générale :
Masque des détails = Image prétraitée - Image prétraitée rendue floue
Image traitée = A . Image prétraitée + B . Masque des détails
où A, un nombre, est la proportion de l'image prétraitée dans l'image finale et B la constante d'efficacité du masque des détails.
Il n'est pas forcé d'ajouter le masque des détails de façon linéaire. Il est tout à fait possible de l'ajouter en le "dénivelant" à l'aide d'une fonction mathématique. De bons exemples peuvent être les fonctions exponentielle (exp) et logarithmique (ln, log10...). Dans le cas de la fonction logarithmique, les détails de faibles luminances seront privilégiés au dépend de ceux de fortes luminances. On pourra utiliser cette fonction pour les détails dans les nébuleuses... Evidement, les valeurs du masque des détails doivent être comprises dans l'intervalle de définition de la fonction. La formulation générale deviendra donc :
Masque des détails adapté = A . (B + Masque des détails)
Image traitée = C . Image prétraitée + D . ln(Masque des détails adapté) ou
Image traitée = C . Image prétraitée + D . log10(Masque des détails adapté) ou
Image traitée = C . Image prétraitée + D . exp(Masque des détails adapté) ...
où A et B sont des constantes qui permettent d'adapter les valeurs des pixels dans l'interval de définition de la fonction utilisée ; C, un nombre, est la proportion de l'image prétraitée dans l'image finale et D la constante d'efficacité de la correction du masque des détails par une fonction mathématique.
Mais :
. Grâce à quelles opérations va-t-on rendre flou ?
. Quel est le flou optimum pour extraire une échelle de détails ? C'est à cette dernière et principale question que nous essayerons de répondre.
(1) On entend par soustraction d'images, la différence pixel à pixel d'une image à l'autre.
(2) On entend par addition d'images, la somme pixel à pixel d'une image et d'une autre.
1 - LA COURBE GAUSSIENNE
2 - LE PRODUIT DE CONVOLUTION
où
g(x,y) est le résultat de la convolution des deux fonctions ;
Dans notre cas h(x,y) serait :
Le lecteur aura sans doute remarqué que cette formule conduit à une infinité d'opérations donc à une infinité de temps de calcul. L'ordinateur n'appréciant pas les intégrales ni d'ailleurs son propriétaire qui a une durée de vie limitée, il est bon de se ramener à une formulation plus simple par matrices ; d'autant plus qu'une image est bornée et spatialement échantillonnée (nous voulons dire que l'on ne connaît de l'image que K échantillons espacés de a ?m selon deux directions perpendiculaires).
La matrice de convolution contiendra un nombre impair de lignes et colonnes N : 3, 5, 7, ...21... Les termes de la matrice seront des valeurs échantillon de la fonction de convolution. L'opération sur une image se résume alors à déplacer la matrice selon les lignes et les colonnes pour calculer la valeur "sous le terme central" de la matrice, du pixel de l'image convoluée. Les N / 2 lignes et colonnes des bords de l'image ne sont donc pas calculables dans les mêmes conditions car une partie de la matrice est "en dehors" de l'image à convoluer. Pour un lieu donné dans l'image (x,y) où la matrice de convolution est superposée et centrée, le résultat de la convolution s'obtient en additionnant, la multiplication des membres de celle-ci avec la valeur des pixels correspondant de l'image. Le résultat de la convolution sera placé en (x,y), dans le pixel de l'image se superposant au membre central de la matrice. Les calculs peuvent conduire à de grandes valeurs numériques gênantes pour le codage informatique de l'image. Pour ramener la valeur moyenne de l'image convoluée à celle de l'image à convoluer, on a l'habitude de diviser le résultat par la somme des termes de la matrice de convolution. Voici la formule permettant de calculer les membres de la matrice de convolution :
où
N est la dimension de la matrice en pixels.
En posant
Par exemple, voici les coefficients d'une matrice 5x5 avec un écart-type de 1 : N=5, int(5/2)=2, =1, S=6.161
On peut considérer que la gaussienne est convenablement échantillonnée si la dimension de la matrice est d'au moins 4 fois son écart-type en pixels. Cela veut dire que l'on convoluera l'image presque toujours par de grandes matrices. Ces grandes matrices sont évidement coûteuses en temps de calcul. Par exemple, la convolution d'une image 768x512 (soit 764 x 508 = 388.112 pixels calculables) par une matrice 5x5 demande 9.702.800 multiplications réelles et 388.112 divisions réelles soit 10.090.912 opérations sur des réels.
Cette courbe a la propriété de séparabilité des variables. On peut utiliser cette propriété pour diminuer le temps de calcul. Cette astuce consiste à convoluer d'abord l'image selon les lignes, puis le résultat selon les colonnes par une matrice mono-dimensionnelle (ou colonnes puis lignes). En reprenant les exemples ci-dessus la matrice mono-dimentionnelle serait
De plus, la manière de coder informatiquement le calcul permet d'en optimiser sa durée. La meilleure méthode sera l'utilisation de pointeurs que l'on incrementera. On évitera de la sorte autant de multiplications et d'additions que de pixels dont on veut lire ou écrire la valeur, comme lorsqu'on utilise des tableaux (il y a un calcul de l'adresse du membre du tableau à chaque fois que l'on utilise une écriture du style h[i,j]=h[i+1,j+1]*h[i-1,j-1]... dans un programme). La différence de temps de calcul entre deux méthodes de codages peut être très impressionnantes !
SOMMAIRE
I - L'image en informatique
1 - Image BITMAP ou point par point
2 - Image vectorielle
1 - D'abord en astrophotographie argentique !
2 - Et maintenant en imagerie numérique
1 - La courbe gaussienne
2 - Le produit de convolution
1 - Action du traitement sur des détails de différents profils photométriques élémentaires
2 - Pourquoi y-a-t-il création d'artefacts ?
III - PRINCIPE GENERAL DU MASQUE FLOU EN IMAGERIE NUMERIQUE
Le principe du masque flou est extrêmement simple. Il s'agit de créer à partir d'une image prétraitée (corrigées de la précharge, du courant d'obscurité, de la plage de lumière uniforme et des différents défauts cosmétiques), une image plus ou moins floue que l'on appelle : le masque flou. En soustrayant le masque flou à l'image prétraitée (1) on obtient pour chaque zone isolée de l'image : les écarts à l'image moyenne de cette zone. Ce sont donc les détails car ils sont très ou légèrement différents de cette image moyenne locale. On peut appeler le résultat de cette soustraction : le masque des détails.
IV - RENDRE FLOU
L'idée qui vient de suite est de mélanger un pixel avec plus ou moins ses pixels voisins. Cette opération mathématique rigoureuse appliquée à chaque pixel de l'image s'appelle le produit de convolution si le mélange d'un pixel avec ses voisins est fait de la même façon pour tous les endroits de l'image. Pour que le flou n'ait pas de direction privilégiée et que l'on puisse facilement paramètrer son importance, on convoluera l'image par une gaussienne ; plus précisément, par une matrice dont les membres sont des valeurs de la gaussienne.
La gaussienne est une courbe très fréquente en physique statistique. Elle est par exemple le profil photométrique d'une étoile sur un capteur à cause de la turbulence atmosphérique, avec un grand temps de pose à l'échelle des temps caractéristiques de la turbulence. Cette courbe est définie, pour une seule variable x, par l'équation :
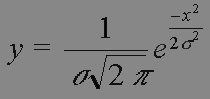
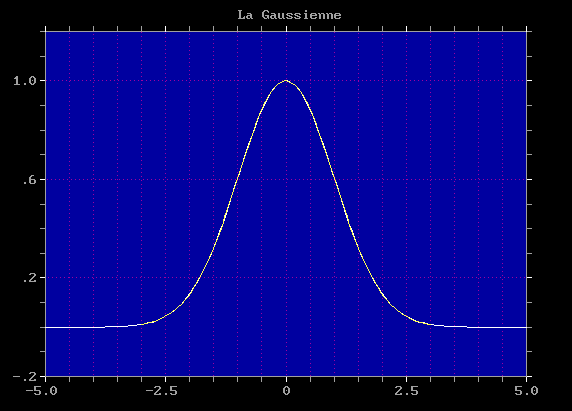
où sigma est l'écart type. Sa représentation graphique est donnée en FIGURE 1. Plus sigma est grand et plus la courbe est "allongée, aplatie", moins "piquée" pour une étoile. Dans notre cas, pour éviter des opérations inutiles, on utilisera la gaussienne en omettant le facteur 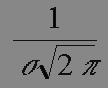 soit l'équation simplifiée
soit l'équation simplifiée 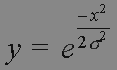 . Le maximum de cette fonction sera alors 1 quand x = 0. A noter que sigma ne doit pas être nul car la fonction n'est pas définie.
. Le maximum de cette fonction sera alors 1 quand x = 0. A noter que sigma ne doit pas être nul car la fonction n'est pas définie.
La convolution est sans doute le calcul le plus utilisé, ainsi que son inverse (la déconvolution) s'il est possible. Il est aussi le plus simple à programmer informatiquement car il se résume à quelques additions et multiplications répétitives. Une formulation mathématique rigoureuse de la convolution bidimensionnelle est :
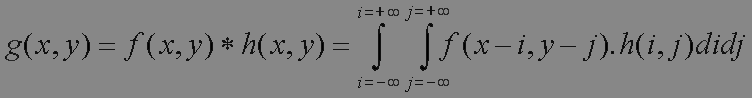
f(x,y) est la fonction à convoluer ;
h(x,y) est la fonction convoluante.
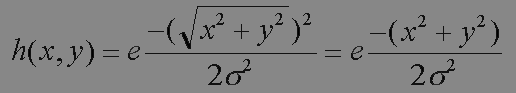
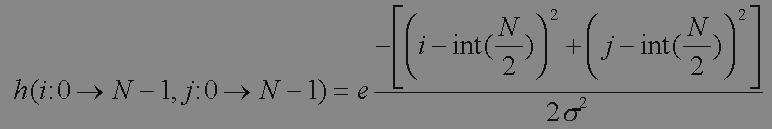
int est la partie entière de l'expression entre parenthèse : int(2.3)=2.
e est l'exponentielle de l'expression.
(sigma) est l'écart-type de la courbe gaussienne.
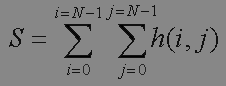 pour le calcul de la somme des termes de cette matrice. On utilisera S comme constante de normalisation des valeurs.
pour le calcul de la somme des termes de cette matrice. On utilisera S comme constante de normalisation des valeurs.
Indice (i,j) i = 0 i = 1 i = 2 i = 3 i = 4 j = 0 1.83e-2 8.20e-2 1.35e-1 8.20e-2 1.83e-2
j = 1
8.20e-2 3.67e-1 6.06e-1 3.67e-1 8.20e-2
j = 2 1.35e-1 6.06e-1 1.0 6.06e-1 1.35e-1
j = 3 8.20e-2 3.67e-1 6.06e-1 3.67e-1 8.20e-2
j = 4 1.83e-2 8.20e-2 1.35e-1 8.20e-2 1.83e-2
La même convolution demandera 3.881.120 multiplications réelles et 388.112 divisions réelles soit 4.269.232 opérations. Soit encore 42.3% d'opérations en moins.
1.35e-1 6.06e-1 1.0 6.06e-1 1.35e-1
 Passer à la suite de l'article
Passer à la suite de l'article
 Page maintenue par David ROMEUF
Page maintenue par David ROMEUF